

賴以威
數學作家、譯者,認為數學不只是助眠跟考試工具,而是一種精準描述的語言。理解數學,就能用另一種更理性與特殊的角度來理解世界。文章散見於《聯合報》《國語日報》《未來少年》數學專欄,著書有《超展開數學教室》《葉丙成的機率驚艷》《再見,爸爸》,曾獲時報文學獎(書簡組),菠羅科學獎(數學)。
新年快樂!雖然傳統氣氛跟電子產品進步成反比,越來越淡薄,但每個人心底還是被習俗深植了一些理所當然:問候語從「你好」變成「新年快樂」,除夕夜全家團圓吃年夜飯等。今年實施一例一休,加班成本提高,某些餐廳或服務業索性春節打烊,讓往年加班的員工能回家過年。
可惜,有個行業沒有減少工時。過年前報到,與前任輪班交接後再也無法休息,站在工作崗位盡心盡力。這是門歷史悠久的職業,員工證前兩號是黃帝欽點應聘的神荼、鬱壘。
滄海之中,有度朔之山,上有大桃木,其屈蟠三千里,其枝間東北曰鬼門,萬鬼所出入也。上有二神人,一曰神荼,二曰鬱壘。主閱領萬鬼。惡害之鬼,執以葦索,而以食虎。於是黃帝乃作禮,以時驅之,立大桃人,門戶畫神荼、鬱壘與虎,懸葦索以御兇魅。——《論衡•訂鬼》
沒錯,今天的主角就是門神,他們被貼在門口阻擋妖魔鬼怪,不管風吹日曬雨淋還是被小孩亂塗鴉都盡忠職守。但業務量顯然超過負荷,幾千年來不斷聘用新人:神荼、鬱壘、秦寶叔、尉遲恭、哼哈二將、四天王、韋馱與伽藍兩大護法、「我一個人就OK了」的鍾馗,中國某些地區除了退休的黃忠,其他五虎將都得上場。台灣還有廟宇找上當年被打跑的荷蘭人,賜他們名為鹿風、耳順,歸化為中華民國國民(正確的說是歸化成中華民國神明,如果是國民的話,年工時從荷蘭人1419小時增加到台灣人的2134小時,可真吃不消)。

 擔任門神的神明眾多,造型也都不盡相同
擔任門神的神明眾多,造型也都不盡相同
台灣目前有856萬戶,不算廟宇店家,光是10%的家戶貼一對門神,就需要高達171萬位門神執勤。勞工權益高漲的現代,我們不僅該替自己爭權益,更應該推己及人,替無法發聲的門神爭取權益,協助他們降低工時。
§
要降低門神工時,首先得釋放對門神的諸多限制。傳統門神工作型態消極,只能在妖魔鬼怪想闖進來時拿兵器一擋:
「哎哎,誰准你進來的。」
如果妖魔鬼怪掉頭改闖隔壁,礙於法規門神也只能請鄰居自求多福。我們不該再有這種自掃門前雪的限制,上古時代神荼、鬱壘管理萬鬼,當門神後要他們拉個板凳只能坐門口,屁股還不能離開板凳,太說不過去了。
我們建議還給門神自由。
倘若看到幾公尺外有隻鬼,他們可以像警察那樣上前盤查:
「青色皮膚的那位,就你啦,大過年的在幹嘛,證件拿出來一下,閻羅王沒蓋章啊?」
拒絕臨檢的還可以動用神權執法。消息在鬼怪之間流傳開來,只要視線內有門神,鬼怪必然不敢輕舉妄動,不再像往常一樣只要門口沒門神就敢亂闖。
得以起身抓鬼後,門神的守備範圍從「戶」拓展成「區」,不用每家每戶門口都有人站崗,大大減少執勤人數。但既然不用站在每家門口,下一個要討論的問題是:站哪兒呢?
答案是,路口。
站在路口得以縱觀四方,一次看好幾條路。問題是路口也有好幾個,以下面這張街道圖來說:
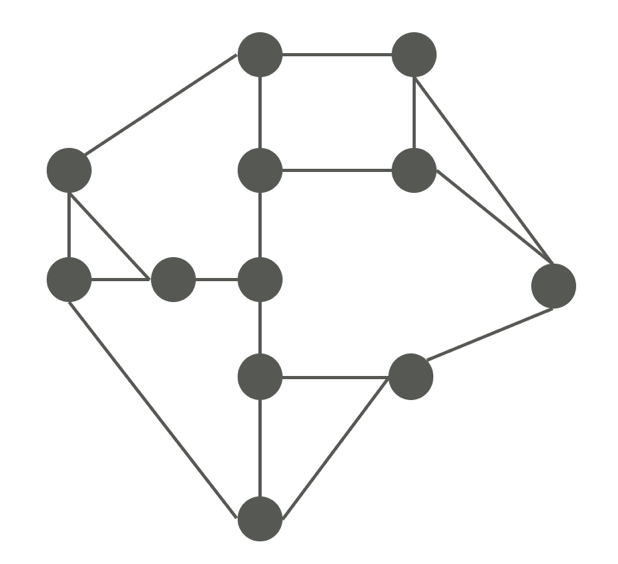
一共有12個路口,我們可以直接擺12對門神,搞得好像玉皇大帝微服出巡,到處都是門神便衣,但這又違背了「降低門神工時」的訴求。
該是請出數學的時候了。
圖論(graph theory)中的點覆蓋(vertex cover)告訴我們,以這個區域來說,只要7對門神就可以確保「每條路至少有一對門神在監視」,是原本每個路口都放門神數的58%。
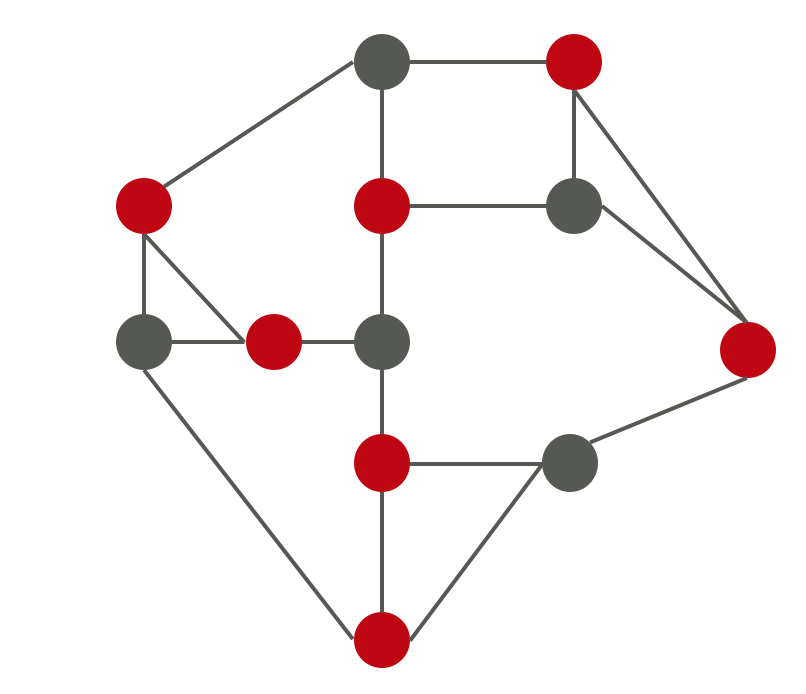
如果是以下的區域,7個路口裡門神站3個路口就足夠,僅需要43%的人力即可。
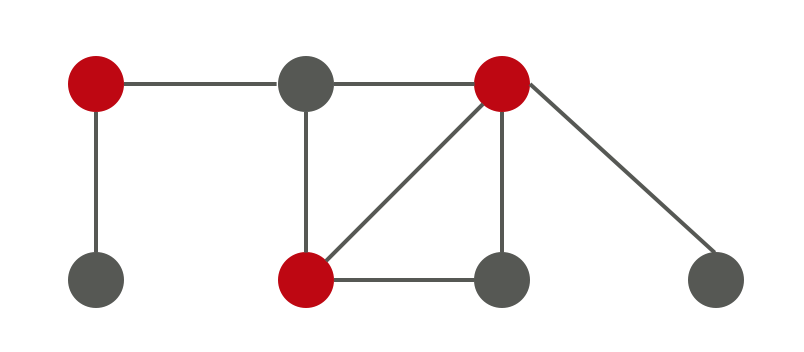
§
圖論是一個聽起來很難,但其實只要會玩「連連看」就能入門的數學知識。圖論的基本元素是「點」與「線」。以門神值勤規劃來說,點是能安排門神站崗的路口,線是街道。「最少點覆蓋(minimum vertex cover)」問題所研究的就是:
找出最小的點集合,讓每條線至少連接上該點集合中的一個點⋯⋯醒醒!這不是數學課!讓我們換成比較好理解的說法:
「找出要哪些路口站崗,才能用最少數量的門神,確保每條街道都至少有一對門神在守護。」
§
看到這邊很多人可能會覺得,「那應該很簡單,交給數學家去規劃就好了。」
事實上數學家的確是認真研究了「最少點覆蓋(minimum vertex cover)」問題,得到的答案是「這問題很複雜,一定可以找到答案,但恐怕得花上很長的一段時間,事實上這是個NP hard⋯⋯」好的我們不再講下去了,不然門神減少目標還沒達成,先成功讓讀者變少了。
基於最佳解很複雜,在此提供各位兩種比較簡單的方案。第一個方案很直覺,每次安排門神時,都跟他說:
「你就去連接街道數目最多,且還沒有其他門神在的那個路口。」
這方法稱為貪婪演算法,有些時候管用有些時候效果不太好。以上面第一張街道圖來說,每個路口都接了三條路,這方法還沒辦法用。
另一個方法是先隨便選定一條路,在兩端路口各擺上一對門神。接著,既然門神在那兒了,凡是這兩對門神守護得到的街道,都先暫時從街道圖上抹去,包括剛剛選的那條路。再從剩下的街道中隨便挑一條,一樣請兩對門神站在該條路的兩端點,刪去這兩對門神可以守護得到的街道。
反覆執行上面的步驟,直到街道圖上一條路都不剩。
如此的門神配置法同樣不是最佳,但最多只會用到2倍的門神數目,這也是數學可以證明的。
§
「生活中到底哪裡有X跟Y啦!」
很多人抱怨數學,是因為不喜歡數學的抽象,在生活中看不到。但脫離考試的折騰後,我們會發現正因為數學夠抽象,才能在不同領域中看見它的應用。今年春節如果看到路口上的電線桿被貼上門神,不妨在附近繞繞看,說不定會發現有人已經在施展運用數學的「最少門神覆蓋術」了。
(歡迎至網頁右上角點選訂閱OKAPI電子報)
點此看賴以威專訪 數學很簡單,因為你不知道生活有多難




























回文章列表