《鋼之鍊金術師》的故事中,想發動鍊金術時,構築鍊成陣的基本要素是「圓形」。
身為人造人的父親大人,為了製造國土鍊成陣,花了快400年,併吞周圍的國家,讓亞美斯多利斯(アメストリス,Amestris)這個國土形狀不規則的小國慢慢擴大,變成接近圓形的國家。
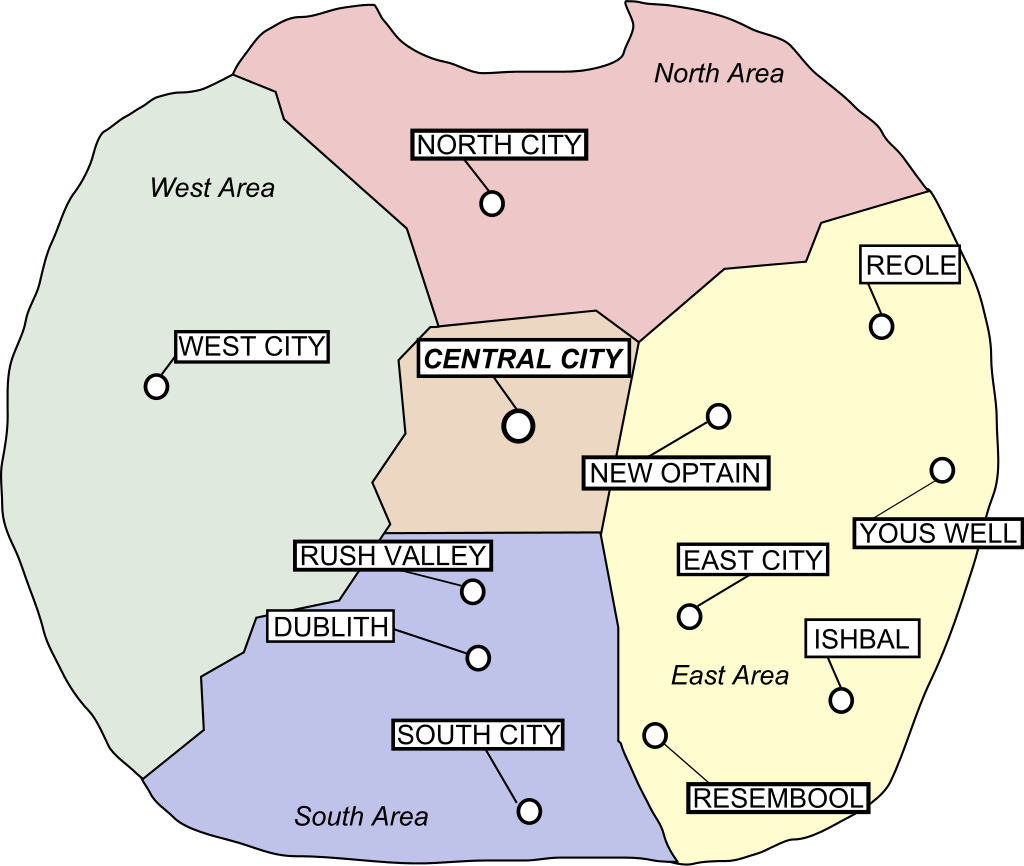 《鋼之鍊金術師》中亞美斯多利斯地圖。(圖/wiki)
《鋼之鍊金術師》中亞美斯多利斯地圖。(圖/wiki)
雖然這樣確實能打造出一個圓形國家,但是隨著計劃拉長,得冒著戰爭失敗、國土無法變成圓形,甚至是被併吞或被革命推翻的風險。
其實,父親大人還能有個更簡單的做法──找個夠圓的國家占領後,再成為總統。
暫時成為迷人的反派,讓我們用數學幫父親大人找個夠圓的國家吧!
§怎麼樣才夠圓?
地球上有許多接近正圓的地區,例如美國佛羅里達州天然形成的金仕萊湖(Kingsley Lake),推測因為當地的石灰岩長期受地下水溶解塌陷後,形成了渾圓的「滲穴」;或者是人們為了找出微小粒子而打造的費米實驗室,但這些地形和建設多半都位於一國之內,而非一個國家的邊界。
如果把範圍限縮到國家的話,那接近「圓形」的國家選擇就少多了。
在地球上的上百個國家中,有些國家的國土形狀看起來明顯不是圓,例如台灣和日本都屬於偏細長型的國土,而國土極度狹長的智利,又比日本和台灣更不「圓」一點。但是,如果國界是像波蘭和法國這種並不狹長的的國土,到底誰比較圓呢?似乎就有點難分高下。
要怎麼衡量一個形狀有多圓呢?
簡單來說,就是看某個形狀與「完美的圓」相差多少,進而測量該形狀的「真圓度(Roundness)」。
一個方法是找出圖形的內接圓和外接圓,再算出兩圓的差距;另一個方法只是找內接圓(或外接圓),再測量該形狀上任一點與內接圓的最遠距離。
或者,也可以從面積來看。
§世界上最圓的國家
曾經有人評選過地球上最圓的國家。
他的評選方法很直覺,在該國國土上隨機找一個點,以射中的點為圓心,畫一個圓。接著,從圓面積和國土面積當中,選擇較大的作為分母;分子則是國土和圓重疊的面積。
嘗試完所有可能的圓心和圓半徑後,找出這個比例的最大值,越接近1,代表圓和國土的交集越大,越接近圓。
根據這個算法,世界上最圓的國家是位在西非的獅子山共和國。不過,儘管獅子山的國界夠圓,人口數卻只有682萬人左右,根據劇情設定,要達成父親大人的計畫,需要像亞美斯多利斯一樣有5000萬人口的國家,而在前幾名圓的國家中,正屬波蘭最接近5000萬人。
考量到鋼鍊的設定大量參考了歐洲近代史,網路上也有許多猜測,討論亞美斯多利斯跟哪個國家最接近,或許透過數學,我們這次找到了一個新的答案。[註1]
§父親大人沒想到的事
在鍊金術的世界裡,既沒有Google Earth,可能也沒有出現像數學王子高斯的天才發明精確的國土測量方法[註2],事實上即使出現天才,大概也都去當鍊金術師了(牛頓表示,我是數學家兼鍊金術師啊)。
沒有數學家、測量學家和地理學家的幫忙,要精確找出世界上的每個國家的真圓度,實在不容易,也辛苦了父親大人。
不過,獲知一部份真理的父親大人,居然從來沒想過佔領一個夠圓的國家來實現他的野望。搞不好這樣的結局,早就在真理的算計之中了吧?
作者簡介
生活數學教育品牌,由臺師大衍生的教育新創企業。曾入選遠見天下文化教育基金會「未來教育臺灣一百」、親子天下「教育創新100」獎項。實施逾百場國小數學實驗課,廣受學生及家長喜愛,獲中央社、大愛電視台等媒體專訪。獲國立臺灣科學教育館與多所國高中邀請舉辦教師研習、家長講座、資優班課程、寒暑假營隊,累積約15,000人次參與。
在Facebook上累積超過12萬名的追蹤者,逾千篇原創內容文章,題材契合新課綱數學素養、跨域學習的潮流,受到許多媒體平台轉載,授權合作媒體包括:聯合報、中央社、TVBS、三立新聞、商業周刊、ETtoday新聞雲等。
2020年5月成立全台唯一以數學科普為主題的YouTube頻道,每週上傳主題多元影片,包含數學實驗、時事分析、數學家人物故事、數學教育議題、推薦書籍或教具。
延伸閱讀



 金仕萊湖(圖/
金仕萊湖(圖/ 費米實驗室衛星圖,圖左下的大圈是兆電子伏特加速器。(圖/
費米實驗室衛星圖,圖左下的大圈是兆電子伏特加速器。(圖/ 獅子山共和國地圖。(圖/
獅子山共和國地圖。(圖/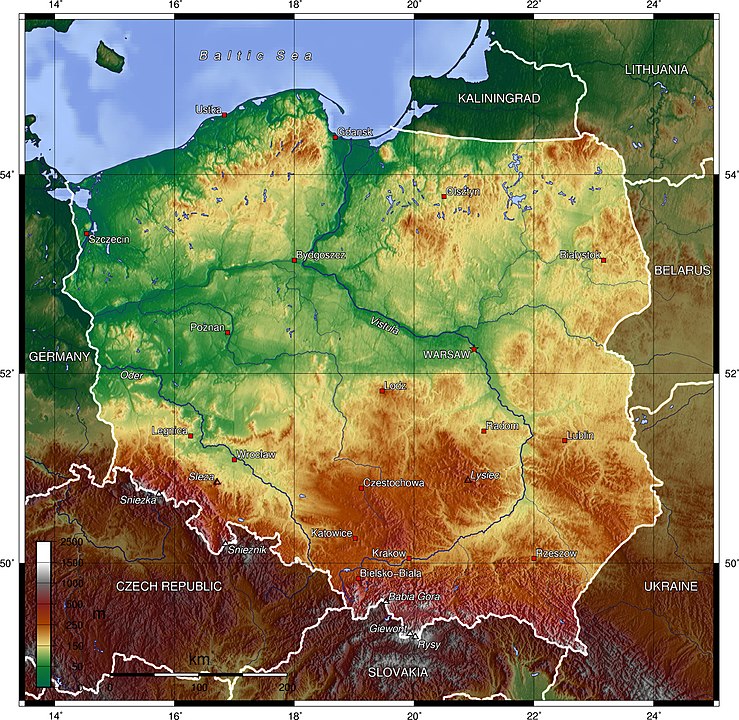 波蘭地圖。(圖/
波蘭地圖。(圖/






















回文章列表